|
In science classes, and anywhere outside of the United States, we measure length with the metric system. The most common units that we use to measure length in this system are the millimeter, centimeter, meter, and kilometer. This Concept will give you an overview of each measurement unit. Let’s take a look at each.
Millimeter The millimeter is the smallest commonly used unit in the metric system. When we measure something in millimeters, we use mm as an abbreviation for millimeter. A millimeter would be used to measure something that is very small, like a seed. Centimeter The centimeter is the next smallest unit of measurement. To abbreviate centimeters we write cm(for example, 3 cm). Centimeters are even smaller than inches. One centimeter is only the width of a staple. This ruler shows centimeters on the bottom and inches on the top. (Inches are not metric so we will not use them in science.
We can use a ruler to measure centimeters and millimeters. On many rulers, we can see both the customary units of measurement and the metric units of measurement. You can see inches, centimeters and millimeters on this ruler. What about when we have to measure something that is longer than a ruler? When we are measuring something that is longer it doesn’t make sense to use centimeters or millimeters. We could use them, but it would take a very long time to count all of those centimeters or millimeters. Instead, we can use two larger units of measurement. We can use the meter and the kilometer.
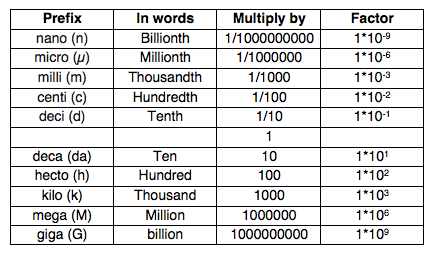
Meters The next metric unit we use is the meter. To abbreviate the meter we write m (for example, 8 m). A meter is longer than a foot. Actually, a meter is just about the same length as a yard. One meter is roughly the length from your foot to your hip. It actually takes 100 centimeters to equal one meter. We use meters to measure bigger objects or longer distances, such as the depth of a pool or length of a hallway. We could use a meter stick to measure meters. A meter stick is exactly one meter long. This is a bit complicated, however, when an object or distance is several meters long. We have to make a mark on the object being measured at the end of the meter stick, then move the meter stick down and make another mark to show the next meter. It is easier to use a tape measure. Tape measures often show customary units (feet and inches) down one side and metric units (centimeters and meters) down the other. What about when we want to measure much longer distances and it doesn’t make sense to use meters? That is when we use kilometers. Kilometers Kilometers are very long. To abbreviate the word kilometer we write km (for example, 12 km). Like miles, we use kilometers to measure long distances, such as the distance from your house to the store or from one town to another. Kilometers are only a little more than 1/2 as long as miles, but they are much longer than meters. In fact, there are 1,000 meters in a kilometer! All of the above measurements are for LENGTH. You might notice that they each contain the word "meter" that is because length is measured in meters. You can also use the metric system when measuring mass or volume. Mass is measured in grams while volume is measured in liters. The prefixes we used for length can also be applied to mass and volume measurements. If one centimeter is 1/100th of a meter, then one centigram is 1/100th of a gram. The prefix tells you how many of the main measurement you have. Kilo = thousand, so a kilogram is going to be 1000 grams while a kilometer is going to be 1000 meters and a kiloliter is going to be 1000 liters. See how it works? Below is a table that shows the relationship between the prefixes.
Converting between metric units is pretty easy once you have some practice. Below is a video you can watch to help you learn some techniques for converting.
1 Comment
What if you went to the grocery store and bought 3 gallons of milk? Could you determine how many pints of milk you purchased? Or how about if you bought 16 pints of milk? How many gallons would this be? In this Concept, you'll learn to make conversions like these so that you can solve real-world problems.
Real-world information is given in dimensions, or the units in which the value is measured. For example, the following are all examples of dimensions.
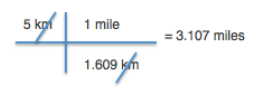
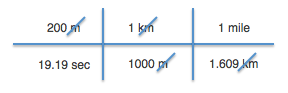
Example 1: lets imagine you have been training for a running race and you know you can run 3 miles. Your friend wants you to sign up for a 5km race. Can you run that distance? First you have to convert km to miles so you can compare the distance of the race to the distance you know you can currently run. You know that 1 mile = 1.609 kilometers. But how can you use this to convert the race distance to miles? Here is one way you can set up the problem.
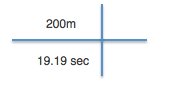
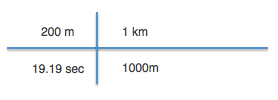
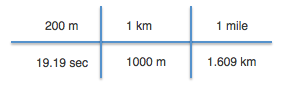
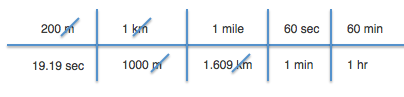
Example 2: Lets try another one. Usain Bolt ran 200 meters in 19.19 seconds. But how many miles per hour is that speed? (miles per hours is abbreviated MPH). We are going to use the same method as above. There are just a few more steps.
4. Remember: when arranging the conversions you always need the units to cancel out. So if the meters is on the top at the beginning then in the next step the meters have to go on the bottom. You can now cross out the units that cancel out.
5. But we aren't done yet. We still need to convert from seconds to hours. We can add this directly to the equation we already have. We know that there are 60 seconds in 1 min (thats the first conversion to add) and we know that there are 60 minutes in 1 hour (thats the second conversion to add).
6. We can now cross out all the units that cancel out. In the end we are left with just the MILES and just the HOURS. Which is exactly what we wanted to convert into.
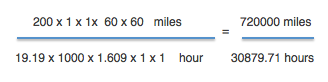
7. Now it is time to multiply the numbers on top together and multiply the numbers on the bottom together.
8. If we simplify this we will get:
9. And if we simplify it one more step we get:
So if you see Usain Bolt running on the road by the school he would actually be SPEEDING as he would be traveling at 23.32 MPH while the speed limit in a school zone is 20 MPH.
Below is a video to watch that will hopefully make this easier. The second video is for solving harder conversions in which you have to convert more than one unit (like the second example above). |
To play the soup game you must add random ingredients until you receive instructions to make conversions.
|